Decoding 101 Financial Alpha Strategies: A Parsing Approach

In this post your will read about:

• Evaluating method for 101 Financial Alphas (expressions) using the Lark parser library.

• Converting alpha expressions into executable Python code for alpha signal generation.

• Way how we implemented alpha signal generation in the QuantJourney backtesting engine.

We all are testing various strategies on our data to determine how to make them profitable. Today, I will show you how I parse the strategies outlined in the document '101 Formulaic Alphas' by Zura Kakushadze, published in December 2015 (https://arxiv.org/pdf/1601.00991) to be an input signal to QuantJourney Backtesting engine. These formulas are derived from real-life quantitative trading alphas. They generate returns for those who trade them, and some are still in use. heir average holding period by author ranged approximately from 0.6 to 6.4 days, and their returns were strongly correlated with volatility.

For QuantJourney code, we must convert it into a numerical string to enable calculations. We'll utilize the Lark parser library, which provides a straightforward grammar for evaluating complex strings. Expressions are defined as functions that accept market data as input and generate alpha values as output.

Once they are numerical, we will incorporate them into our config file for the Backtesting engine and run them on our dataset alongside other parameters for OrderEvent and MarketEvent, etc.

Strategies

I have coded all the strategies into JSON format, here are a few:

"1": "(rank(ts_argmax(signedpower(((returns < 0) ? stddev(returns, 20) : close), 2.), 5)) - 0.5)", 
"2": "(-1 * correlation(rank(delta(log(volume), 2)), rank(((close - opens) / opens)), 6))", 
"3": "(-1 * correlation(rank(opens), rank(volume), 10))", 
"4": "(-1 * ts_rank(rank(low), 9))", 
"5": "(rank((opens - (sum(vwap, 10) / 10))) * (-1 * abs(rank((close - vwap)))))", 
"6": "(-1 * correlation(opens, volume, 10))", 
"7": "((adv20 < volume) ? ((-1 * ts_rank(abs(delta(close, 7)), 60)) * sign(delta(close, 7))) : (-1* 1))", 
"8": "-1*rank(((sum(opens, 5)*sum(returns, 5))-delay((sum(opens, 5)*sum(returns, 5)),10)))", 
"9": "((0 < ts_min(delta(close, 1), 5)) ? delta(close, 1) : ((ts_max(delta(close, 1), 5) < 0) ? delta(close, 1) : (-1 * delta(close, 1))))", 
"10": "rank(((0 < ts_min(delta(close, 1), 4)) ? delta(close, 1) : ((ts_max(delta(close, 1), 4) < 0) ? delta(close, 1) : (-1 * delta(close, 1)))))", 

Considering the complexity of financial expressions, a well-defined grammar is crucial for accurate parsing and analysis. These expressions frequently encompass a range of functions and operations, including mathematical calculations, statistical measures, and time series manipulations. As such, the Lark grammar must be both comprehensive and robust to handle these intricacies. Here is a part of it:

delay: "delay" "(" value "," SIGNED_NUMBER ")"
delta: "delta" "(" value "," SIGNED_NUMBER ")"

correlation: "correlation" "(" value "," value "," SIGNED_NUMBER ")"
covariance: "covariance" "(" value "," value "," SIGNED_NUMBER ")"

factory: "factory" "(" FACTORY_STRING ["," FACTORY_STRING ] ")"

self_attribute: "self." CNAME

close: "close"
opens: "opens"
high: "high"
low: "low"
volume: "volume"
returns: "returns"
vwap: "vwap"
adv: "adv" SIGNED_NUMBER
cap: "cap"

number: SIGNED_NUMBER

ts_max: "ts_max" "(" value "," SIGNED_NUMBER ")"
ts_min: "ts_min" "(" value "," SIGNED_NUMBER ")"
ts_argmax: "ts_argmax" "(" value "," SIGNED_NUMBER ")"
ts_argmin: "ts_argmin" "(" value "," SIGNED_NUMBER ")"
ts_rank: "ts_rank" "(" value "," SIGNED_NUMBER ")"
stddev: "stddev" "(" value "," SIGNED_NUMBER ")"

So now having grammar, to evaluate each alpha, we have created two primary classes in our code: AlphaExpressionsand AlphaFactor.

1. AlphaExpressions: This class handles the transformation of alpha expressions into executable commands.

2. AlphaFactor: This class manages the parsing of expression strings using Lark and generates the pipeline code for calculating alpha values.

We will use the following Python libraries:

• Lark: This parsing library allows us to define the grammar for alpha factor expressions and parse these expressions into a tree structure. The grammar is defined in a separate file, "alpha_expression.lark", and is loaded into the code. Lark provides a convenient way to set syntax rules for the expressions and generates a parse tree based on these rules.

• Six: This library enables iteration over dictionary key-value pairs in a version-independent manner.

Now, let’s see key methods used:

AlphaExpressions Class

This class is responsible for converting parsed expressions into Python code that can compute alpha values. Here's a look at some of the key methods:

• init(): Initializes the transformer with default parameters.

• datasource(items): Processes data source items.

• neg(items): Handles negation operations.

• rank(items): Handles rank operations.

• cap(items): Handles cap operations.

• number(items): Processes numeric items.

• close(items): Handles close price items.

• high(items): Handles high price items.

• low(items): Handles low price items.

• volume(items): Handles volume items.

• vwap(items): Handles VWAP items.

• adv(items): Handles ADV items.

• opens(items): Handles open price items.

• div(items): Handles division operations.

• min(items): Handles minimum operations.

• max(items): Handles maximum operations.

• powerof(items): Handles power operations.

• signedpower(items): Handles signed power operations.

• minus(items): Handles subtraction operations.

• plus(items): Handles addition operations.

• mult(items): Handles multiplication operations.

• log(items): Handles logarithm operations.

• abs(items): Handles absolute value operations.

• sign(items): Handles sign function operations.

• scale(items): Handles scaling operations.

• greaterthan(items): Handles greater-than comparison operations.

• lessthan(items): Handles less-than comparison operations.

• equals(items): Handles equality comparison operations.

• logicalor(items): Handles logical OR operations.

• ternary(items): Handles ternary conditional operations.

• returns(items): Handles returns operations.

• delta(items): Handles delta operations.

• delay(items): Handles delay operations.

• ts_max(items): Handles time-series maximum operations.

• ts_min(items): Handles time-series minimum operations.

• ts_argmax(items): Handles time-series argmax operations.

• ts_argmin(items): Handles time-series argmin operations.

• ts_rank(items): Handles time-series rank operations.

• stddev(items): Handles standard deviation operations.

• sum(items): Handles sum operations.

• product(items): Handles product operations.

• correlation(items): Handles correlation operations.

• covariance(items): Handles covariance operations.

• decay_linear(items): Handles linear decay operations.

Let's go through an example to better understand the step-by-step process:

"24": "((((delta((sum(self.close, 100) / 100), 100) / delay(self.close, 100)) < 0.05) || ((delta((sum(self.close, 100) / 100), 100) / delay(self.close, 100)) == 0.05)) ? (-1 * (self.close - ts_min(self.close, 100))) : (-1 * delta(self.close, 3)))"

alpha_factor = AlphaFactor(strategy_expr)
alpha_factor.parse()
alpha_factor.transform()						      # Transform the parsed tree
alpha_factor.generate_pipeline_code()			# Generate the pipeline code

• The main() function loads the strategy expressions from the strategies_json string into a dictionary called strategies.

• For each strategy ID and expression in strategies, the script creates an instance of the AlphaFactor class, passing the expression as an argument.

• The parse() method of the AlphaFactor class is called, which uses Lark to parse the expression based on the defined grammar. The resulting parse tree is stored in the tree attribute of the AlphaFactor instance.

• The transform() method is called, which creates an instance of the AlphaExpressions class and transforms the parse tree into a sequence of commands and data requirements. The AlphaExpressions class is a transformer that walks through the parse tree and generates the necessary commands and data inputs for the alpha factor calculation.

• The generate_pipeline_code() method is called to generate the final pipeline code for the strategy. It combines the transformed commands, data inputs, and necessary imports into a single string, which represents the executable code for the alpha factor.

• Finally, the generated pipeline code is printed for each strategy - which uses our prime functions (added to the code) to calculate per input data (OHLCV) value of the certain Alpha.

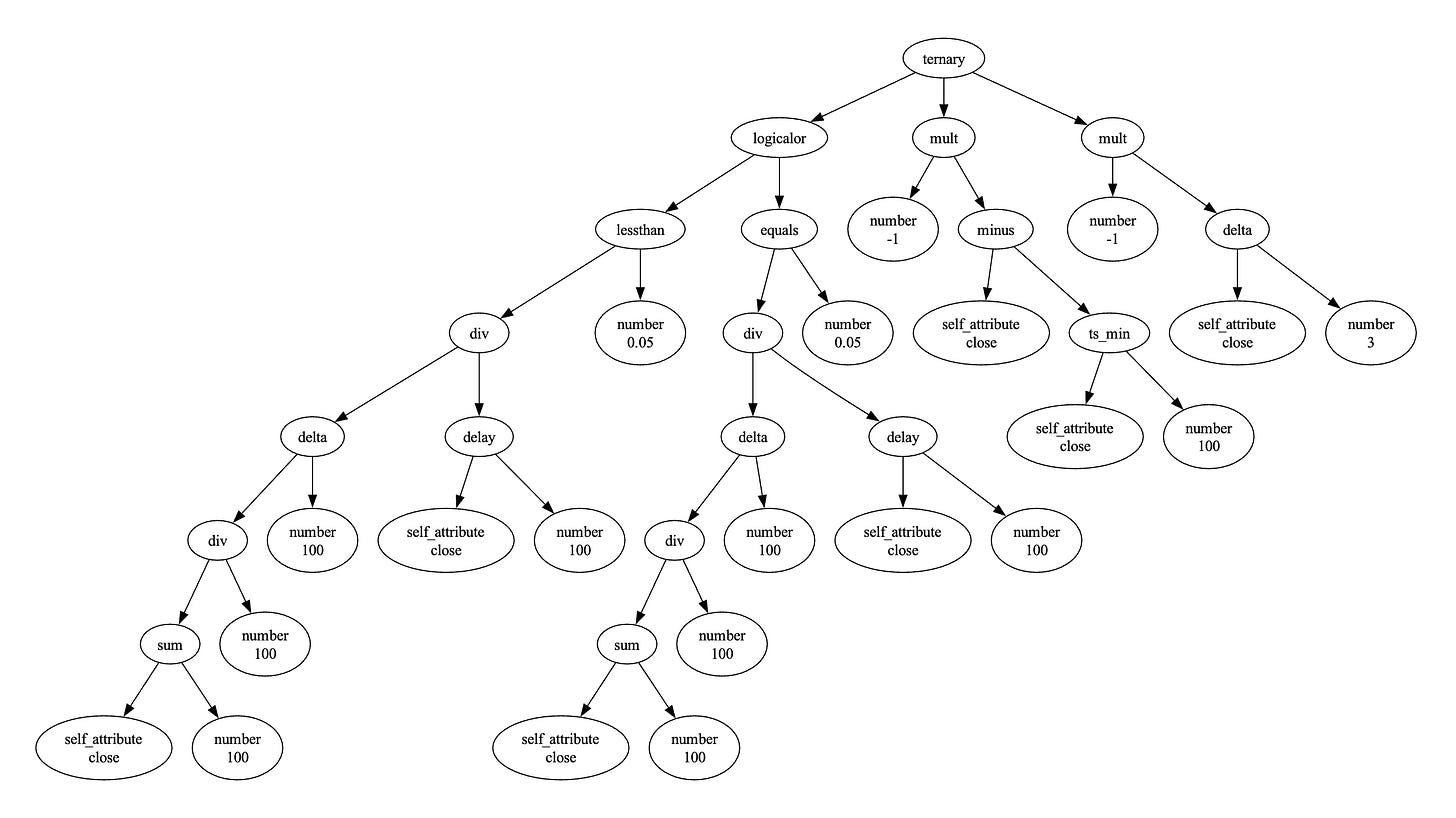
Here, you can see the Tree as output from Lark, using the specified grammar.

Processing strategy 24: ((((delta((sum(self.close, 100) / 100), 100) / delay(self.close, 100)) < 0.05) || ((delta((sum(self.close, 100) / 100), 100) / delay(self.close, 100)) == 0.05)) ? (-1 * (self.close - ts_min(self.close, 100))) : (-1 * delta(self.close, 3))):

Parse tree: ternary
  logicalor
    lessthan
      div
        delta
          div
            sum
              self_attribute    close
              100
            number      100
          100
        delay
          self_attribute        close
          100
      number    0.05
    equals
      div
        delta
          div
            sum
              self_attribute    close
              100
            number      100
          100
        delay
          self_attribute        close
          100
      number    0.05
  mult
    number      -1
    minus
      self_attribute    close
      ts_min
        self_attribute  close
        100
  mult
    number      -1
    delta
      self_attribute    close
      3

['return ((-1 * (self.close - ts_min(self.close, 100))) if (((delta((ts_sum(self.close, 100) / 100), 100) / delay(self.close, 100)) < 0.05) or ((delta((ts_sum(self.close, 100) / 100), 100) / delay(self.close, 100)) == 0.05)) else (-1 * delta(self.close, 3)))']

And the plot how the tree looks like:

SignalEvents in QuantJourney Backtesting Engine

These strings are then inputted into the SignalsEvent class for the Backtesting Engine, as configured in the JSON file:

"events_engine_params" : {
				"signal_events_params": {
					"signals_params": {
								"buy_signals": {
									"SMA_10_50_crossover": "SMA(10) > SMA(50)"
								},
								"sell_signals": {
									"SMA_10_50_reverse_crossover": "SMA(10) < SMA(50)"
								}
					},
					"rules_params": {
								"simple_crossover": {
									"description": "A simple crossover",
									"buy": "SMA_10_50_crossover",
									"sell": "SMA_10_50_reverse_crossover"
								}
					}
				},

The SignalEvent is a component of the EventEngine in the QuantJourney Backtester, which is built on an event-driven approach. Essentially, an event-driven architecture enables the system to react to events as they occur, instead of adhering to a sequential flow.

1. Events: Everything that happens is treated as an event. Examples include new market data, signals generated by a strategy, orders sent to the broker, and orders filled.

2. Event Loop: An event loop continuously checks for and processes events. This loop ensures that events are handled in a timely manner. Events are typically processed by an event loop or an event handler that dispatches them to the appropriate components.

3. Event Handlers: The system consists of event producers (e.g., data sources, strategies) and event handlers (e.g., order execution, risk management) that communicate through events. Eachhandler responds to events relevant to its functionality.

In the context of backtesting, events represent different stages or actions within the trading process.

• In QuantJourney Backtesting engine have types of events: MarketEvent, SignalEvent, and OrderEvent.

  MarketEvent represents the arrival of new market data, such as macro updates or fundamental changes, for a specific symbol at a given datetime.

  SignalEvent represents a trading signal generated by a strategy for a specific symbol at a given datetime. It includes the strategy and the signal type (e.g., buy, sell).

  OrderEvent represents an order to be placed in the market, specifying the symbol, order type e.g. stop-loss, take-profit or more complex like triple-band, or range-breakout-order.

I will elaborate on this in future posts and share the relevant code.

# ActionType class -------------------------------------------------------------------
class ActionType(Enum):
	LIQUIDATE = 'liquidate'								# sell the entire position
	OPEN_LONG = 'open_long'								# open a long position
	REDUCE_LONG = 'reduce_long'							# reduce the size of a long position
	PARTIAL_CLOSE = 'partial_close'						# sell a part of the position
	HOLD = 'hold'										# hold the current position
	SCALE_IN = 'scale_in'								# scale into a position (buy more)
	SCALE_OUT = 'scale_out'								# scale out of a position (sell some)
	HEDGE_POSITION = 'hedge_position'					# hedge a position (e.g., with options)
	ROLL_POSITION = 'roll_position'						# roll a position forward
	PLACE_LIMIT_ORDER = 'place_limit_order'				# place a limit order (buy or sell)
	PLACE_STOP_ORDER = 'place_stop_order'				# place a stop order (buy or sell)
	MARKET_EXIT = 'market_exit'							# exit at the market price (buy or sell)
	REBALANCE_PORTFOLIO = 'rebalance_portfolio'			# rebalance the portfolio (e.g., based on weights)
	CANCEL_PENDING_ORDER = 'cancel_pending_order'		# cancel a pending order (limit or stop)
	ADJUST_LEVERAGE_RATIO = 'adjust_leverage_ratio'		# adjust the leverage ratio

# OrderType class -------------------------------------------------------------------
class OrderType(Enum):
	STOP_LOSS = 'stop_loss'								# stop-loss order
	TAKE_PROFIT = 'take_profit'							# take-profit order
	BUY_STOP_LIMIT = 'buy_stop_limit'					# buy stop-limit order
	SELL_STOP_LIMIT = 'sell_stop_limit'					# sell stop-limit order
	TRAILING_STOP_LOSS = 'trailing_stop_loss'			# trailing stop-loss order
	TRAILING_STOP_LIMIT = 'trailing_stop_limit'			# trailing stop-limit order
	TRAILING_TAKE_PROFIT = 'trailing_take_profit'		# trailing take-profit order
	LIMIT_ENTRY = 'limit_entry'							# limit entry order
	STOP_ENTRY = 'stop_entry'							# stop entry order
	VOLATILITY_POSITION_SCALE = 'volatility_position_scale' # volatility-based position scaling order
	TIME_EXIT = 'time_exit'								# time-based exit order
	CONDITIONAL_ENTRY = 'conditional_entry'				# conditional entry order
	RANGE_BREAKOUT_ENTRY = 'range_breakout_entry'		# range breakout entry order
	REBALANCE = 'rebalance'								# rebalance order (e.g., based on frequency)
	VOLUME_BASED = 'volume_based'						# volume-based order (e.g., based on threshold)
	MARKET_ON_CLOSE = 'market_on_close'					# market-on-close order (e.g., for end-of-day)
	CUSTOM = 'custom'

And part of EventEngine Class:

# EventEngine class --------------------------------------------------------
class EventEngine:
	def __init__(self, config: Dict[str, Any]):
		"""
		Initialize the EventEngine with the specified configuration and data handler.

		Args:
			config (Dict[str, Any]): Configuration options for the EventEngine.
			data_handler (DataHandler): The data handler object for accessing market data.
		"""
		self.config = config
		self.config_OrderEvent = config.get("order_events_params", {})
		self.config_MarketEvent = config.get("market_events_params", {})
		self.config_SignalEvent = config.get("signal_events_params", {})
		self.market_event = MarketEvent(self.config_MarketEvent)
		self.signal_event = SignalEvent(self.config_SignalEvent)
		self.order_event = OrderEvent(self.config_OrderEvent)
		self.positions = {}								# Dictionary of positions per instrument (e.g. long, short, flat)
		self.orders = {}							    # Dictionary of orders per instrument (e.g., stop-loss, take-profit)

	def generate_events(self,
						instrument: str,
						market_data: pd.DataFrame,
						strategies: Dict[str, str],
						market_regime_data: pd.Series
						) -> Tuple[List[MarketEvent], List[SignalEvent], List[OrderEvent]]:
		"""
		Generate market events, signal events, and order events.
		Market events are agnostic to strategy, while signal and order events are strategy-specific.

		Args:
			current_date (pd.Timestamp): The current date.
			market_data (Dict[str, pd.DataFrame]): A dictionary containing historical market data per instrument.
			market_regime_data (pd.Series): A Series containing the market regime data.

		Returns:
			Tuple[List[MarketEvent], List[SignalEvent], List[OrderEvent]]: A tuple containing the generated market events, signal events, and order events.
		"""
		market_events = self.market_event.generate_market_events(market_data)

		signal_events_df = pd.DataFrame()
		order_events_df = pd.DataFrame()

		for strategy in strategies:
			signal_events_df = self.signal_event.generate_signal_events_single_strategy(market_data, strategy)
			order_events_df = self.order_event.generate_order_events(market_data)

		return market_events, signal_events_df, order_events_df

Conclusion

With the completed AlphaFactor class and the previously defined AlphaExpressions class, we now have a comprehensive framework for parsing and evaluating financial alpha expressions using Lark. This implementation ensures that complex financial expressions are correctly interpreted and converted into executable Python code, facilitating robust alpha signal generation for trading strategies.